επόμενο:Προσπίπτουσα ηλιακή ροή στη Γη

προηγούμενο:Φασματικά χαρακτηριστικά ακτινοβολίας

ενότητα:Η Γη ως πλανήτης

Μεταβολές της ηλιακής ακτινοβολίας

Για ένα άστρο που γεννήθηκε από μικρή μάζα, όπως ο ήλιος, οι φάσεις της εξέλιξης του είναι οι εξείς :

Σώμα μεγάλης έκτασης με 1000 K που εκπέμπει ισχυρά στην περιοχή του υπέρυθρου. Το πρωτόαστρο σιγά σιγά συμπυκνώνεται και η θερμοκρασία του πυρήνα αυξάνεται.

Οταν το πρωτόαστρο συμπυκνωθεί αρκετά, η θερμοκρασία του πυρήνα του είναι αρκετά υψηλή ( K) για να αρχίσουν οι θερμοπυρηνικές αντιδράσεις σύντηξης. Η ροή ενέργειας που ακτινοβολείται από την επιφάνεια αναπληρώνεται από την πυρηνική ενέργεια, που προέρχεται από την καύση υδρογόνου σε ήλιο (He).

Η επιφάνεια είναι αρκετά ζεστή και ακτινοβολεί στο ορατό. Αυτή η φάση του άστρου είναι η κύρια φάση της εξέλιξης του και είναι μακροπρόθεσμη σταθερή και ήσυχη.

Η ακτινοβολία και η θερμοκρασία καθορίζονται από τη μάζα του άστρου. Οσο πιο μεγάλη είναι η μάζα, τόσο πιο ισχυρή είναι η ακτινοβολία, και άρα πιο σύντομος ο θάνατος. Αστρα που γεννήθηκαν από πρωτόαστρα μεγάλης μάζας, διαρκούν πιο λίγα χρόνια ως άστρα της κύριας ακολουθίας.

Ο ήλιος, που γεννήθηκε από πρωτόαστρο μικρής μάζας, καίει υδρογόνο για έτη, και θα συνεχίσει για ακόμα έτη σε αυτή τη φάση.

Οταν εξαντληθεί το υδρογόνο τότε ο Ηλιος υφίσταται θεμελιώδεις αλλαγές. Ο πυρήνας του άστρου καταρρέει ενώ η ατμόσφαιρα του εκτείνεται σε μέγεθος 100 . H θερμοκρασία του πυρήνα μεγαλώνει αρκετά για να μετατρέπεται το ήλιο (Ηe) σε άνθρακα (C). To άστρο αποτελείται από ένα μικρό πυρήνα και μια τεράστια ατμόσφαιρα μικρότερης θερμοκρασίας, δηλαδή εκπέμπει στα κόκκινα μήκη κύματος.

Αν έχει αρκετή μάζα ο Ηλιος θα μπορούσε να φτάσει σε φάση καύσης του άνθρακα. Δεν έχει όμως αρκετή μάζα και έτσι όταν εξαντληθεί το ήλιο η ατμόσφαιρα του θα ξεχωρίσει από τον πυρήνα και θα γίνει ένα πλανητικό νεφέλωμα το οποίο φωτοβολείται από ένα κεντρικό Ασπρο Νάνο, ο οποίος σιγά σιγά κρυώνει και πεθαίνει.

Η λαμπρότητα L του σημερινού Ηλιου μπορεί να εκφραστεί σαν συνάρτηση της εσωτερικής πυκνότητας ενέργειας :

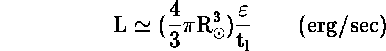
όπου είναι ο χαρακτηριστικός χρόνος διαρροής ενέργειας από τον Ηλιο. Οπως είδαμε :

και έτσι :

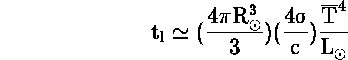
όπου είναι η μέση εσωτερική θερμοκρασία, η οποία μπορεί να υπολογιστεί κατά προσέγγιση ως εξής:

Από την εξίσωση κίνησης έχουμε :

όπου p είναι η πίεση σε απόσταση r από το κέντρο του Ηλιου, ρ είναι η πυκνότητα, Μ(r) είναι η μάζα που περιέχεται εντός ακτίνας r και G η σταθερά της παγκόσμιας έλξης.
Η μάζα M(r) δίνεται από :

και έτσι αν ορίσουμε μια μέση πυκνότητα σαν :

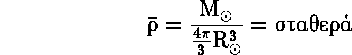
Εχουμε =1,409 gm/ όπου gm και cm.

Τότε

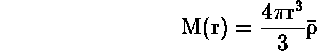
και

Με την οριακή συνθήκη p=0 σε r= έχουμε :

Αν υποθέσουμε ότι η μέση πίεση και θερμοκρασία ισχύουν για r= /2 τότε :

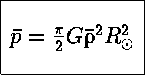
Για να υπολογίσουμε τη μέση θερμοκρασία , χρησιμοποιώ την καταστατική εξίσωση τελείου αερίου:

όπου n είναι η πυκνότητα αριθμου των σωματιδίων (αριθμός/όγκο) του αερίου και k είναι η σταθερά του Boltzmann. Η πυκνότητα μάζας ρ μπορεί να εκφραστεί σαν :

για ένα καθαρό αέριο, όπου μ είναι το μοριακό βάρος (μετρημένο σε μάζες πρωτονίου). Δηλαδή

Για ένα μίγμα υδρογόνου και ηλίου (από τα οποία αποτελείται ο Ηλιος), η πυκνότητα του υδρογόνου είναι :

και του ηλίου είναι :

όπου το είναι το κλάσμα της μάζας του υδρογόνου (προς την ολική μάζα) και το κλάσμα της μαζας του ηλίου, και προφανώς . Το είναι η πυκνότητα αριθμού των πυρήνων υδρογόνου, και η αντίστοιχη πυκνότητα αριθμού για το ήλιο. Στο εσωτερικό του Ηλιου το υδρογόνο και το ήλιο είναι εντελώς ιονισμένα, κι έτσι αφού κάθε άτομο υδρογόνου έχει ένα πυρήνα και ένα ηλεκτρόνιο, για κάθε πυρήνα έχουμε δυό σωματίδια.Ομοια, για κάθε πυρήνα ηλίου έχουμε τρία σωματίδια, αφού σε κάθε πυρήνα ηλίου αντιστοιχούν 2 ηλεκτρόνια. Αρα η ολική πυκνότητα αριθμού είναι :

Αντικαθιστώντας τα και έχουμε :

αλλά και και , όπου είναι το του μίγματος των αερίων. Αρα:

το οποίο δίνει :

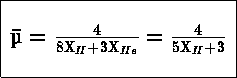
(για τελείως ιονισμένο μίγμα αερίων).

Ετσι

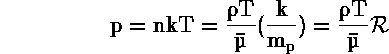
όπου = k/ =σταθερά, που ονομάζεται

Η μέση θερμοκρασία του εσωτερικού τότε είναι :

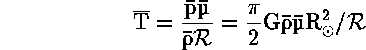
όπου,

= 1,402 gm/

= 4/(3+5 )=0,59 για =0,75

G = 6,67 /gm

= 8,314 erg/gm K

= 6,96 cm

Αντικαθιστώντας έχουμε K.

Μπορούμε τώρα να υπολογίσουμε το χαρακτηριστικό χρόνο διαρροής ενέργειας από τον Ηλιο :

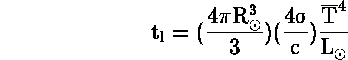
όπου 4σ/c= erg/ και

/3 = 1,412

ενώ erg/sec. Τότε έχουμε :

sec ή 6.6 έτη

Δηλαδή μια μεταβολή στην παραγωγή ακτινοβολίας εντός του Ηλιου, παίρνει χρόνια για να επηρεάσει τη λαμπρότητα. Η ολική ακτινοβολία που εκπέμπει ο Ηλιος είναι σχεδόν σταθερά σε κλίμακα γήινου χρόνου.

Ο χαρακτηριστικός χρόνος διαρροής είναι μιά περίπλοκη συνάρτηση της εσωτερικής δομής του Ηλιου. Θεωρίες μεταφοράς ακτινοβολίας σε ιονισμένο αέριο δίνουν :

Ετσι :

Από την εξίσωση κίνησης βλέπουμε ότι και αφού τότε .

Επιπλέον έχουμε p=nkT που δίνει , έτσι . Αλλά ρ=n μ ρ/μ. Ετσι βρίσκουμε ότι :

Αρα :

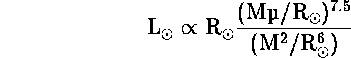
ή τελικά

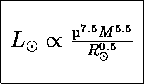
Η κύρια διεργάσια παραγωγής ενέργειας μέσα στον Ηλιο είναι η σύντηξη 4 πυρήνων υδρογόνου σε έναν πυρήνα ηλίου.

Η μάζα ενός πυρήνα υδρογόνου είναι ενώ η μάζα του πυρήνα του ηλίου είναι 3,97 . Υπάρχει ένα έλλειμα μάζας Δm=0,03 . Αυτό το ποσό μάζας έχει μετατραπεί σε ενέργεια:

Βλέπουμε ότι από μιά μάζα 4 παράγεται 0,03 ενέργεια.

Οσο προχωρεί η καύση του υδρογόνου, το κλάσμα της μάζας του υδρογόνου προς την ολική μάζα μειώνεται και το μέσο μοριακό βάρος αυξάνεται. Επειδή βλέπουμε ότι η λαμπρότητα αυξάνεται όσο καίγεται το υδρογόνο.
Η ηλικία του Ηλιου σαν άστρο της κύριας ακολουθίας (δηλ. σε φάση που καίει υδρογόνο), είναι της τάξης των 5 ετών. Η ηλικία της Γης είναι 4,5 έτη. Ας υποθέσουμε ότι η λαμπρότητα του Ηλιου ήταν σταθερή σ΄ αυτό το χρονικό διάστημα.Τότε η ολική ενέργεια που έχει ακτινοβοληθεί είναι :

όπου είναι η ηλικία του Ηλιου σαν άστρο της κύριας ακολουθίας. Αρα η μάζα του υδρογόνου που έχει μετατραπεί σε ήλιο, ( ), είναι

Η μάζα αυτή αποτελεί ένα κλάσμα της ολικής μάζας, η οποία έχει μειωθεί μόνο επί 0,007 . Μπορούμε να υποθέσουμε ότι η μάζα του Ηλιου ήταν σταθερή σ΄αυτή την περίοδο. Το μέσο μοριακό βάρος όμως αυξήθηκε.

Το σημερινό κλάσμα ενώ του πρωτόγονου Ηλιου ήταν περίπου :

έτσι

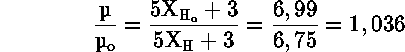
Eίδαμε ότι η μάζα παρέμενε σταθερή, οπότε αν αγνοήσουμε αλλαγές στην ακτίνα του Ηλιου τότε :

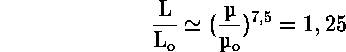
Η λαμπρότητα του πρωτόγονου Ηλιου ήταν μόνο 0,77 της σημερινής τιμής. Πιο αναλυτικά μοντέλα δίνουν τη θερμοκρασία σα συνάρτηση του χρόνου :

όπου είναι η σημερινή λαμπρότητα του Ηλιου, και η ηλικία του σαν άστρο της κύριας ακολουθίας. Στο t=0, η λαμπρότητα του πρωτόγονου Ηλιου ήταν

Δηλαδή ήταν κατά 30 % πιο αδύνατος όσον αφορά τη λαμπρότητα.

Μοντέλα κλίματος δείχνουν ότι για κάθε 1 % μείωση στη λαμπρότητα του Ηλιου αντιστοιχεί μιά μείωση 1 Κ στη θερμοκρασία της γήινης επιφάνειας. Αυτό δείχνει ότι η Γη έπρεπε να ήταν 30 Κ πιο κρύα. Η σημερινή μέση θερμοκρασία της Γης είναι περίπου 288 Κ (15 βαθμοί Κελσίου), πράγμα που σημαίνει ότι η πρωτόγονη Γη είχε μέση θερμοκρασία 258 Κ (-15 β. Κελσίου). Η Γη ήταν τελείως παγωμένη.
Αντίθετα, από την ύπαρξη λιθικών στρωμάτων ηλικίας της τάξης των ετών, που δημιουργήθηκαν από ιζηματαγένεση στη Γροινλανδία, βγάζουμε το συμπέρασμα ότι υπήρχε αύθονο επιφανειακό νερό. Αυτή η ασυνέπεια μεταξύ της θεωρίας της εξέλιξης του Ηλιου και τα γεωλογικά δεδομένα, ονομαζεται
Το παράδοξο μπορεί να συμβιβαστεί, αν υποθέσουμε ότι, η ατμόσφαιρα της πρωτόγονης Γης περιείχε πιο πολύ διοξείδιο του άνθρακα από ότι έχει σήμερα και έτσι επικρατούσε ένα πιο έντονο φαινόμενο Θερμοκηπίου.

επόμενο:Προσπίπτουσα ηλιακή ροή στη Γη

προηγούμενο:Φασματικά χαρακτηριστικά ακτινοβολίας

ενότητα:Η Γη ως πλανήτης