επόμενο:Kατανομές ιχνοστοιχείων

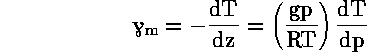
προηγούμενο:Κορεσμένη πίεση υδρατμού

ενότητα:Στοιχεία της ατμόσφαιρας    

Θερμοβαθμίδα για υγρό αέρα

Για να υπολογιστεί η θερμοβαθμίδα της ατμόσφαιρας όταν περιέχει υδρατμό πρέπει να βρεθεί μια έκφραση για dT/dp επειδή έχομε:

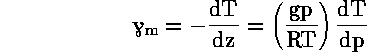
όπου dp/dz=-gρ. Σύμφωνα με τον δέυτερο νόμο της θερμοδυναμικής για αντιστρεπτή διεργασία έχομε:

όπου S είναι η εντροπία (erg/K) του συστήματος. Απο τον πρώτο νόμο της θερμοδυναμικής dQ=dE + pdV και dH=dE+dpV έτσι:

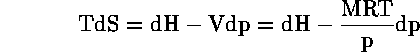
όπου pV=MRT και χωρίς αλλαγή φάσεως (χαφ) τότε αντικαθιστώντας :

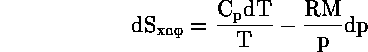
Για νερό ή πάγο τα οποία είναι ουσιαστικά ασυμπίεστα έχομε dp=0 ενώ για τον υδρατμό έχομε μια πηγή εξωτερικής ενέργειας που προέρχεται από την εξαέρωση νερού ή πάγου από την ηλιακή ακτινοβολία. Ετσι για την εντροπία του υδρατμού έχομε δύο συνιστώσες:

όπου:

το παραστάνει την λανθάνουσα θερμότητα για να μετατρεπτεί ένα gm συμπυκνωμένης ύλης (πάγος ή νερό) σε υδρατμό, ενώ το είναι η μάζα που έχει μετατραπεί σε υδρατμό. Η ολική μεταβολή εντροπίας είναι:

όπου οι δείκτες σ, υ και d αντιστοιχούν για συμπυκνωμένη ύλη, υδρατμό και άνυδρο αέρα. Για αδιαβατικές μεταβολές δεν έχομε μεταβολή στην εντροπία, δηλαδή dS=0 και έτσι:

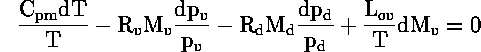
όπου Αν θέσομε όπου και αντικαταστήσομε:

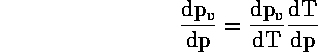
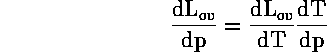
και χρησιμοποιήσουμε την εξίσωση των Clausius-Clapeyron τότε μπορούμε να υπολογίσομε το για οποιασδήποτε ποσότητας υδρατμού στην ατμόσφαιρα. Αν ο υδρατμός είναι ιχνοστοιχείο, δηλαδή η ολική πίεση και , τότε μπορούμε να διαιρέσομε με την παραπάνω εξίσωση της ισεντροπίας και να καταλύξομε στον πρώτο νόμο της θερμοδυναμικής συμπεριλαμβώμενος την ενέργια από την συμπύκνωση του υδρατμού:

Αν υποθέσομε ότι η σχετική υγρασία, η οποία ορίζεται από και έχει τιμή 0 1, είναι σταθερή με ύψος z, τότε έχομε:

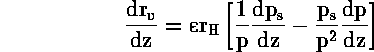
και αντικαταστήσομε:

τότε από την εξίσωση των Clausius-Clapeyron βρίσκομε:

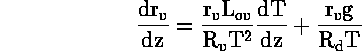
έτσι:

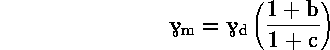
όπου :

Αν θέσομε για την επιφάνεια της Γης = 288 Κ, = 0,77 , p = 1000 mbar και έχομε σταθερές = 0,069 cal/gmK, = 0,24 cal/gmK τότε = 13 mbar , = 0,008, = 589 cal/gm , b = 0,24 και c = 1,25. Ετσι έχομε K/km.

Στην τροπόπαυση = 9,76 K/km γιατί ο υδρατμός συμπυκνώνεται και πέφτει ως βροχή κάτω από το ύψος ( 11,5 km) της τροπόπαυσης. Αν πάρομε ως μέση θερμοβαθμίδα για την τροπόσφαιρα γ = 7,5 K/km τότε στην τροπόσφαιρα η θερμοκρασία σε ύψος z δίνεται από:

και η θερμοκρασία της τροπόπαυσης Τ = 213 K. Aν υπολογίσομε την μέση τιμή της θερμοκρασίας στην τροπόσφαιρα ως = ( ) = 251 K τότε βλέπομε ότι είναι σχέδον η ίδια με την ενεργό θερμοκρασία της Γης που υπολογίσαμε στο Πρώτο Κεφάλαιο.

επόμενο:Kατανομές ιχνοστοιχείων

προηγούμενο:Κορεσμένη πίεση υδρατμού

ενότητα:Στοιχεία της ατμόσφαιρας