επόμενο:Φάση Ξήρανσης

ενότητα:Αποθέματα Νερού   

Φάση 'Υγρανσης

Ο ταμιευτήρας υποδοχής αποτελείται τη συνολική επιφάνεια που υποδέχεται τον ημερήσιο υετό. Για την i-μέρα η ποσότητα αυτή νερού P προστίθεται στην ήδη υπάρχουσα:

Το πλεόνασμα U αποτελεί το υπόλοιπο του κατακριμνήσματος, που είτε προσέπεσε από τη βλάστηση στο έδαφος, είτε κατευθείαν μπήκε στον ταμιευτήρα επιφάνειας. Για την ημερήσια μεταβολή στο περιεχόμενο D τού τελευταίου ισχύουν ανάλογες σχέσεις:

με V να ορίζεται ως το ημερήσιο πλεόνασμα του ταμιευτήρα επιφάνειας.

Αν την i-μέρα ο ρυθμός F κατείσδυσης στο έδαφος είναι F V , τότε όλο το πλεόνασμα, αν υπάρχει, θα κατευθυνθεί προς τα κάτω. Στην αντίθετη περίπτωση V F η διαφορά V F που δε θα κατεισδύσει θα απομακρυνθεί ως επιφανειακή απορροή R . Ειδικότερα, μάλιστα:

Προφανώς αν υπάρχει απορροή (R 0), μετά θα είναι .

Αυτός καθ' εαυτός ο F θα εξαρτάται από το ποσό νερού S που περιέχει ο ταμιευτήρας εδάφους, καθώς με ταμιευτήρα γεμάτο ο ρυθμός F θα ελαχιστοποιείται, ενώ με ξερό έδαφος θα πρέπει να έχουμε ένα μέγιστο ρυθμό κατείσδυσης F . Αυτές οι διαπιστώσεις μάς οδηγούν να περιγράψουμε τον F με απλό τρόπο με τη βοήθεια μιας συνάρτησης της μορφής:

με k > 0. Ο ελάχιστος ρυθμός F του F θα προκύπτει, είπαμε, όταν S=S. Αυτό με τη σειρά του σημαίνει τα εξής:

• O ρυθμός διήθησης p προς το υπέδαφος αποκτά μια τιμή p=p. Αν, μάλιστα, το υπέδαφος είναι ξερό (G=0) , τότε ο ρυθμός διήθησης θα έχει γίνει μέγιστος p=p .
• Η εσωτερική απορροή από το έδαφος θα έχει γίνει μέγιστη.

Αναλυτικότερα για τα δυο παραπάνω μεγέθη μπορούμε να παρατηρήσουμε:

Ο ρυθμός διήθησης θα φροντίζει να αναπληρωθεί το νερό που απορρέει από το υπέδαφος και, όπως μόλις είπαμε, θα αποκτά μια μέγιστη τιμή στην ειδική περίπτωση που έχει κορεστεί ο υπερκείμενος S και έχει αδειάσει ο υποκείμενος G. 'Αρα ο p θα έχει τη μορφή:

αγνοώντας την ποσότητα νερού που τυχόν αντλείται για άρδευση ή χάνεται, η οποία προσθαφαιρείται, όπως σύντομα θα δούμε, κατευθείαν από την ποσότητα G.

'Οσον αφορά στην εσωτερική απορροή από το έδαφος, θεωρούμε ότι αυτή γίνεται με διαφορετικό ρυθμό κοντά στην επιφάνεια απ' ότι σε βαθύτερα στρώματα. Συγκεκριμένα σε μικρό βάθος ένα ποσοστό , από το κλάσμα του νερού F που κατεισδύει στο έδαφος, απορρέει γρήγορα προς την επιφάνεια. Αυτή ορίζουμε ως πρώτη μερική απορροή εδάφους subf1:

Με ανάλογο τρόπο ένα ποσοστό , προερχόμενο από μεγαλύτερο βάθος, απορρέει αργότερα. Η συνιστώσα αυτή ορίζεται ως η δεύτερη μερική απορροή εδάφους subf2:

Ισχύει προφανώς ότι: . Η εξάρτηση αυτών των επιμέρους ροών από το τετράγωνο του λόγου είναι μια αυθαίρετη επιλογή, που η αναγκαιότητά της φάνηκε σε μια συγκεκριμένη εφαρμογή του μοντέλου που χρησιμοποιεί τον παρόντα συλλογισμό. Η δύναμη που υψώνεται ο λόγος αυτός έχει τη χροιά παραμέτρου που καθορίζεται κατά βούληση ανάλογα με τις συνθήκες που εξετάζουμε. Τα αποτελέσματα που προκύπτουν αποτελούν το γνώμονα για την ορθότητα κάθε επιλογής.

Επανερχόμενοι στην ελάχιστη τιμή F του F, σύμφωνα με όσα αναφέραμε, είναι:

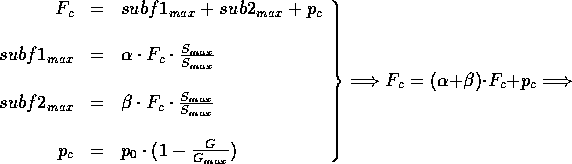
και από τη (2.6) υπολογίζουμε την άγνωστη παράμετρο k:

Γνωρίζοντας τα παραπάνω μπορούμε να βρούμε πώς μεταβάλλεται το νερό εδάφους S με το χρόνο. Η εξίσωση που περιγράφει τη διαδικασία είναι η εξής:

όπου

Με τη μέθοδο ολοκλήρωσης Euler-Τραπεζίου είναι απλό να γίνει η ολοκλήρωση της (7.12) πάνω σε διάστημα μιας ημέρας και να υπολογιστεί ο ζητούμενος ρυθμός. Θα είναι λοιπόν για την i-μέρα και για Δt = 1 ημέρα:

Aκριβώς ανάλογα υπολογίζεται και ο ρυθμός μεταβολής Β του νερού υπεδάφους G. Η εξίσωση περιγραφής του φαινομένου είναι εδώ:

Με ολοκλήρωση της (7.14) και για Δt = 1 ημέρα, θα είναι το νερό υπεδάφους G την i-μέρα:

Οι εξισώσεις (7.5) ως και (7.7), (7.12) και (7.14) ως και (7.16) επιλύονται για την κάθε i-μέρα με την επαναληπτική μέθοδο Newton-Raphson. Τότε, γνωρίζοντας σε καθημερινή βάση τις τιμές των F , S και G , υπολογίζονται τελικά οι μερικές απορροές εδάφους R και υπεδάφους R :

Η εκροή, ωστόσο, στο σημείο της εξόδου της λεκάνης απορροής (που είναι και το σημείο στο οποίο γίνονται οι πειραματικές μετρήσεις) δεν είναι το άθροισμα των δυο αυτών μερικών απορροών. 'Οπως προαναφέρθηκε, οι R και R υπόκεινται σε καθυστερήσεις, τις οποίες μπορούμε να παραστήσουμε με τη μορφή δυο ταμιευτήρων καθυστέρησης Τ και Τ . Για καθέναν από αυτούς η τελική εκροή Q δίνεται για την i-μέρα από την απλή μορφή:

Οι συντελεστές κ , κ , είναι παράμετροι της προσομοίωσης και λειτουργούν πάνω στα αντίστοιχα περιεχόμενα των ταμιευτήρων ως εξής: Για την i-μέρα

και το ζεύγος εξισώσεων (7.19) γίνεται:

Προφανώς ισχύει για τους a, b ότι: και . Oι συντελεστές a, b εξαρτώνται από τα ιδιαίτερα τοπογραφικά χαρακτηριστικά της εκάστοτε περιοχής που εξετάζεται. Από τη χρήση τους συνάγουμε ότι όσο μεγαλύτερη είναι η τιμή κάποιου από αυτούς, τόσο περισσότερο διευκολύνει την εκροή, αφού αυξάνει την τιμή του Q και παράλληλα (από τις (7.20), (7.21)) αποθαρρύνει τη συγκέντρωση νερού στον ταμιευτήρα καθυστέρησης που ανταποκρίνεται. Οι τιμές των a, b καθορίζονται κατά τέτοιον τρόπο, ώστε να δίνουν την επιθυμητή καθυστέρηση σε κάθε μια από τις απορροές R και R που τους αντιστοιχούν.

 

επόμενο:Φάση Ξήρανση

ενότητα:Αποθέματα Νερού