επόμενο:H Γη ως μη ιδανικό μέλαν σώμα

ενότητα:Η Γη ως πλανήτης   

Μεταβολές της ροής λόγω τροχιάς

Η μέση ηλιακή ροή που προσπίπτει στη Γη είναι η ηλιακή σταθερά :

σε μονάδες όπου είναι η μέση απόσταση Ηλιου-Γης. Η απόσταση αυτή αλλάζει επειδή η τροχιά της Γης είναι ελλειπτική. Τα στοιχεία ελλειπτικής τροχιάς είναι:
Σημείο S : ο Ηλιος, Σημείο Α : το περιήλιο, Σημείο Β : το αφήλιο, Απόσταση CA : μεγάλος ημιάξονας, Απόσταση CD : μικρός ημιάξονας και e=CS/CA=0,0167 : η εκκεντρότητα.

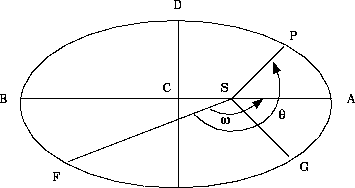
Σχήμα 1.7 Τα στοιχεία ελλειπτικής τροχιάς

Αν θέσουμε a=CA και b=CD, τότε η εξίσωση της τροχιάς είναι :

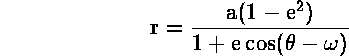
όπου = ηλιακό μήκος και = μέσο μήκος του περιηλίου.
Οι ορισμοί των και περιγράφονται στο ακόλουθο διάγραμμα, που δείχνει την τροχιά του Ηλιου με κέντρο τη Γη.
, <PFP'= δ = ηλιακή απόκλιση, , FGF'G' = επίπεδο εκλειπτικής, FLF'L' = επίπεδο ουράνιου ισημερινού, Σημείο Ε = Γη, και Σημειο Α = περιήλιο.

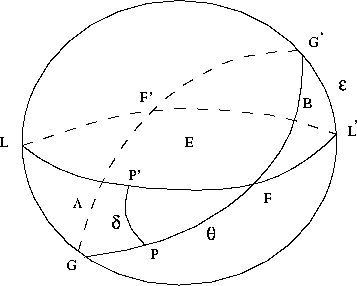
Σχήμα 1.8 Επίπεδο εκλειπτικής

Για τα σημεία F,G,A,F',G',B :

Από τον δευτερο νόμο του Kepler έχομε :

όπου Α είναι το εμβαδόν επιφάνειας που διαγράφει η ακτίνα της τροχιάς και αν υποθέσομε ότι το r σχέδον σταθερό (λόγω της μικρής εκκεντρότητας) τοτε

ετσι

οπου P είναι η περίοδος της τροχιάς και αν n είναι οι ημέρες του χρόνου από την 1η Ιανουαρίου τότε :

και έτσι όταν n=1, , δηλαδή έχουμε περιήλιο.
Η ηλιακή απόκλιση δ δίνεται από :

και η μέγιστη τιμή ονομάζεται της εκλειπτικής, και έχει τιμή .

Η μέση απόσταση =a=μεγάλος ημιάξονας τροχιάς, και έτσι έχουμε :

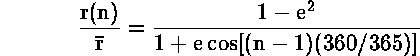
Η ηλιακή ροή την n-οστή ημέρα του χρόνου είναι :

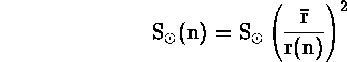
Βλέπουμε ότι η ηλιακή ροή στη Γη υφίσταται μέγιστες αλλαγές της τάξης των 3,5% εντός ενός χρόνου.

Πρέπει επίσης να σημειωθεί ότι η εκκεντρότητα e της τροχιάς δεν είναι σταθερά σε κλίμακα εκατομυρίων χρόνων. Πριν από 500.000 χρόνια ενώ πριν από 700.000 χρόνια ήταν 0,053.

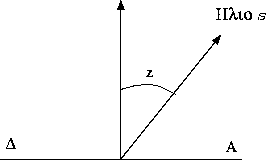
Η προσπίπτουσα ηλιακή ροή εξαρτάται και από την ώρα της ημέρας και την εποχή. Αυτό είναι συνέπεια της συνεχούς μεταβολής του ζενίθ του Ηλιου, δηλαδή της γωνίας που σχηματίζει ο Ηλιος με την κατακόρυφη ευθεία από την επιφάνεια της Γης. Εχομε z=0 κατακόρυφος Ηλιος, z= ανατολή του Ηλιου (Α) και z= δύση του Ηλιου (Δ).

γεωγραφικό πλάτος, <ΡΒΡ'= h="ωριαία" γωνία.

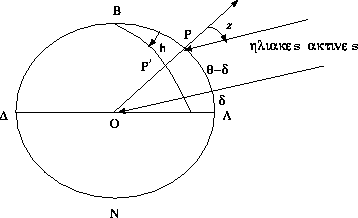
Σχήμα 1.9 Ζενίθ του Ηλιου

Aπό τη γεωμετρία έχουμε :

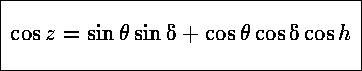
Η ηλιακή απόκλιση καθορίζει τις εποχές, το γεωγραφικό πλάτος, το φως της Ημέρας και η ωριαία γωνία την ώρα της ημέρας.

Εχουμε:
δ=0, ισημερία
0, ο Ηλιος είναι στο Βόρειο ημισφαίριο
0, ο Ηλιος είναι στο Νότιο ημισφαίριο

, για Βόρεια σημεία
, για Νότια σημεία

h=0, μεσημβρία
h<0, προ μεσημβρία (π.μ)
h>0, μετά μεσημβρίας (μ.μ.)

Η ωριαία γωνία δίνεται από h= και τη μετράμε από τα μεσάνυχτα. Οταν t=0, h= και όταν t=24, h= .
όπου t είναι σε ώρες. Το μπορεί να γραφτεί ως :

όπου και
Εξω από τους πόλους, δηλαδή , την ώρα που ανατέλει ή δύει ο Ηλιος, έχουμε :

και έτσι και η ωριαία γωνία δίνεται από :

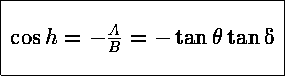
Οι ώρες που ανατέλει και δύει ο Ηλιος, αντιστοχούν σε ωριαίες γωνίες :
h=-H ανατολή του Ηλιου
h=+H δύση του Ηλιου .

Οι αντίστοιχες ώρες της ημέρας είναι :

έτσι

= , όπου :

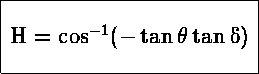
Eπανάληψη των ορίων :
α)
β)
γ)

Εχομε γιατί , και έτσι και

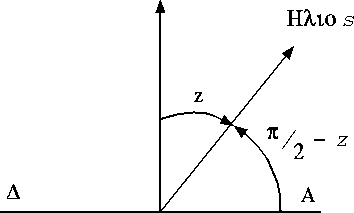
Σχήμα 1.10 Το ύψος του Ηλιου στους πόλους

Η γωνία -z ονομάζεται γωνία ύψους και βλέπουμε ότι είναι ίση με δ. Ετσι όταν δ>0, που διαρκεί για έξι μήνες, ο Ηλιος είναι σε ύψος δ ακτινίων πάνω από τον ορίζοντα. Δηλαδή για έξι μήνες οι ώρες φωτός είναι 24 (συνέχεια ηλιοφάνεια). Αντίθετα στο Νότιο πόλο το ίδιο εξάμηνο έχουμε πάντα σκοτάδι.

Οταν δ=0, έχουμε ισημέρια, εκτός από τους πόλουs, όπου ο Ηλιος κινείται για μιά μέρα πάνω στον ορίζοντα.

Το μεσημέρι έχουμε h=0 και τότε:

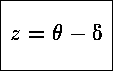
Οταν έχουμε ισημερία δ=0 και z= . Σε πλάτος =0, στον ισημερινό, z=0 και ο Ηλιος είναι κατακόρυφος το μεσημέρι.
Ο Ηλιος είναι κατακόρυφος, δηλαδή z=0, όταν .

Στο θερινό ηλιοστάσιο για το Βόρειο ημισφαίριο, δ= και =δ στον τροπικό του καρκίνου. Εκεί το μεσημέρι ο Ηλιος είναι κατακόρυφος.

Εκτός από τους πόλους ( ) έχουμε:

όπου 24Η/ = ώρες φωτός
Οταν δ=0, δηλαδή στην ισημερία, =0 και Η= /2. Ετσι

Ανεξαρτήτως του γεωγραφικού πλάτους , εκτός από τους πόλους, έχουμε 12 ώρες νύχτα και 12 ώρες ημέρα.

Τη n-οστή μέρα του χρόνου, που ο Ηλιος είναι σε ζενίθ , έχουμε:

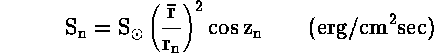
είναι η ηλιακή ροή πάνω στην επιφάνεια της Γης, όπου

και

Ολοκληρώνοντας, για μιά μέρα, έχουμε:

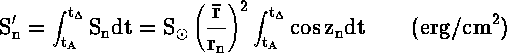
όπου αγνοήσαμε τη μεταβολή του κατά τη διάρκεια μιάς ημέρας. Αν αγνοήσουμε και τη μεταβολή του δ κατά τη διάρκεια μιάς ημέρας, τότε:

όπου έχουμε αντικαταστήσει dh= . Eτσι :

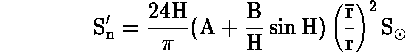
Αλλά ο παράγων 24Η/ = ώρες φωτός και αν ορίσουμε το μέσο ζενίθ του Ηλιου για την ημέρα n σαν:

τότε βλέπουμε ότι:

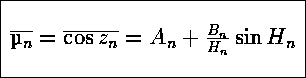
για Το δίνει το μέσο ζενίθ του Ηλιου για την n-οστή μέρα του χρόνου. Αν παραστήσουμε τις ώρες φωτός με , τότε η ολική ηλιακή ροή πάνω στη Γη δίνεται από:

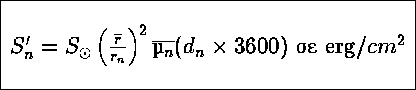
Είδαμε ότι για το μέσο ζενίθ του Ηλιου δίνεται από:

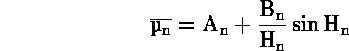
Οταν :

που ισχύει όταν με ή όπου δ>0. Δηλαδή και , όταν . Για , και .

Οταν ο Ηλιος είναι στο Βόρειο ημισφαίριο, δηλαδή δ>0, τότε για πλάτη στο Βόρειο ημισφαίριο, όπου , αν ο Ηλιος δεν βασιλεύει (πολικό καλοκαίρι), ενώ για πλάτη στο Νότιο ημισφαίριο, όπου , αν τότε ο Ηλιος δεν ανατέλλει (πολικός χειμώνας). Οι αντίθετες συνθήκες επικρατούν όταν δ<0, δηλαδή όταν ο Ηλιος είναι στο Νότιο ημισφαίριο. Γενικά, το κρίσιμο πλάτος δίνεται από για πλάτη στο Βόρειο ημισφαίριο και από για πλάτη στο Νότιο ημισφαίριο, όπου .

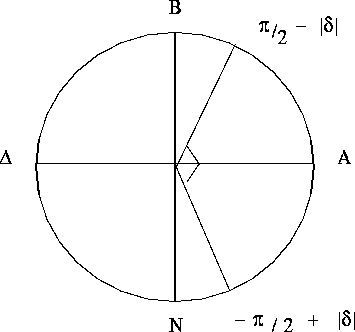
Σχήμα 1.11 Κρίσιμο πλάτος για πολικό καλοκαίρι ή χειμώνα

Βλέπουμε ότι αν τότε οι ώρες φωτός είναι Ετσι για πλάτη όταν μπορούμε να ολοκληρώσουμε το ως εξής:

Ετσι το μέσο ζενίθ για το πολικό καλοκαίρι δίνεται από:

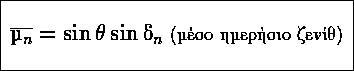
Οταν Η=0, δηλαδή για τον πολικό χειμώνα, έχομε . Eτσι:

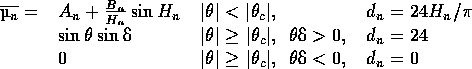
Οταν δ=0, τότε και για έχουμε ισημερία, Η= Στους πόλους και o Ηλιος κάθεται στον ορίζοντα και δεν είναι ούτε μέρα ούτε νύχτα.

   

επόμενο:H Γη ως μη ιδανικό μέλαν σώμα

ενότητα:Η Γη ως πλανήτης