προηγούμενο:Η θερμόσφαιρα
ενότητα:Στοιχεία της
ατμόσφαιρας
Για να καθοριστεί η κατανομή της πιέσεως,
θερμοκρασίας και της πυκνότητας με το ύψος στην
ατμόσφαιρα πρέπει να λύσομε τρείς εξισώσεις που
περιγράφουν την κίνηση της ατμόσφαιρας, την
διατήρηση της ενέργειας στην ατμόσφαιρα και την
καταστατική εξίσωση του αέρα.
Οι κύριες δυνάμεις που καθορίζουν την δομή της ατμόσφαιρας είναι η πίεση και η βαρύτητα. Σε πρώτη προσέγγιση, μπορούμε να αγνοήσομε τις δυνάμεις που προέρχονται από την περιστροφή της Γης και την τριβή του αέρα, και έτσι επικρατεί υδροστατική ισορροπία. Η βαροβαθμίδα τότε δίνεται από:
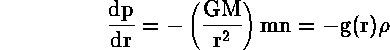
όπου Μ είναι η μάζα του πλανήτη, m είναι η μέση μοριακή μάζα, n είναι η πυκνότητα αριθμού των σωματιδίων του αέρα, ρ είναι η πυκνότητα μάζας, r είναι η απόσταση από το κέντρο της Γης, G είναι η σταθερά παγκοσμίου έλξεως και g(r) είναι η τοπική επιτάχυνση της βαρύτητας. Για ένα τέλειο αέριο η καταστατική εξίσωση δίνει τη σχέση μεταξύ πίεσης και θερμοκρασίας:
όπου R= 
/ 
και είναι η παγκόσμια
σταθερά αερίων ενώ είναι το μέσο μοριακό βάρος του αέρα. H
απόσταση 
όπου 
είναι η
ακτίνα της Γης και z το ύψος από την επιφάνεια της
Γης. Αντικαθιστώντας το 
στην εξίσωση της
βαροβαθμίδας έχουμε:
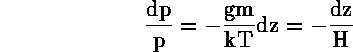
όπου το H= T/ g λέγεται ύψος
κλίμακος και δίνει την απόσταση εντός της οποίας
η πίεση μειώνεται στο 1/e της τιμής της. Aν η
θερμοκρασία είναι σταθερά τότε H=σταθερά και η
πίεση δίνεται από:
όπου p είναι η πίεση όταν z=z. Στην Ομόσφαιρα το Η 
7 
1 km.
Ο πρώτος νόμος της θερμοδυναμικής μπορεί να εκφραστεί ως εξής:
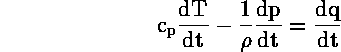
όπου 
είναι η είδικη θερμότητα του αέρα ύπο σταθερή
πίεση και dq είναι η καθαρή θέρμανση ανά μονάδα
μάζας. Η πρώτη έκφραση στα αριστερά της άνω
εξίσωσης καθορίζει τον ρυθμό ψύξης ή θέρμανσης, η
δεύτερη έκφραση είναι η μεταβολή ενέργειας από
εκτόνωση ( ψύξη) ή από συμπίεση (θέρμανση). Οταν η
εξωτερική θέρμανση dq=0 τότε οι μεταβολές στη
θερμοδυναμική της ατμόσφαιρας λέγονται
αδιαβατικές και είναι αντιστρεπτές. Οταν το dq = 0
τότε οι μεταβολές λέγονται διαβατικές και είναι
μη αντιστρεπτές, π.χ. όταν το dq είναι η θέρμανση
από την απορρόφηση ηλιακής ακτινοβολίας.
Yπο αδιαβατικές συνθήκες έχομε:
και αντικαθιστώντας την πυκνότητα μάζας από την
καταστατική εξίσωση βρίσκομε:
όπου R= / και έτσι:
με Α=σταθερά και 
για άνυδρο αέρα.
Συνδυάζοντας την εξίσωση της υδροστατικής ισορροπίας με την αδιαβατική θερμοκρασία έχομε:
άρα :
Η τιμή του
για άνυδρο αέρα είναι 
(erg/gm K) και το g = 981 ( 
). Αν θυμηθούμε
ότι ένα erg = 
τότε
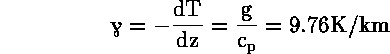
Βλέπομε ότι η θερμοβαθμίδα για 
άνυδρο αέρα εξαρτάται
από τη τιμή της ειδικής θερμότητος υπό σταθερή
πίεση. Αν ο αέρας περιέχει υδρατμό τότε η αυξάνεται και
το γ μειώνεται. Δηλαδή, η ατμοσφαιρική
θερμοκρασία μειώνεται πιό αργά με το ύψος. Οπως
θα δούμε αργότερα, η συμπύκνωση του υδρατμού
είναι πηγή θέρμανσης και από τον πρώτο νόμο της
θερμοδυναμικής αυτό σημαίνει ότι η θερμοβαθμίδα
γ μειώνεται.
προηγούμενο:Η θερμόσφαιρα
ενότητα:Στοιχεία της ατμόσφαιρας